彭实戈 数学家，1947年12月8日出生于山东省滨县（今滨州）。 1974年山东大学物理系毕业， 1974年获巴黎九大３阶段博士， 1986年获法国普鲁旺斯大学（应用数学）博士， 1988-1989年复旦大学博士后， 1992年获法国领导研究资格。中国科学院院士，山东大学教授。现任山东大学数学研究所所长、金融研究院院长。

彭实戈主要从事随机控制理论、概率论、随机分析、金融数学方面的研究和教学工作。以彭实戈为第一负责人的国家自然科学基金委“九五”重大项目《金融数学、金融工程和金融管理》有力地推动了“金融数学”这门新兴学科在中国的发展。

倒向随机微分方程和非线性数学期望

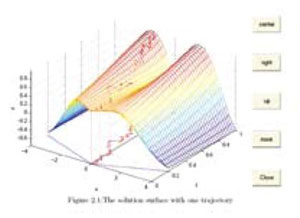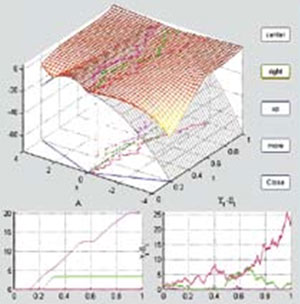
倒向随机微分方程（BSDE）与1942年Ito教授引入的（正向）随机微分方程(SDE)的重要的不同是：SDE由当前确定的初始条件演化出将来的（当前无法确定）的解；而BSDE则由将来的（目前无法确定的终端条件）倒向地计算出当前能够确定的解。

1. 创立倒向随机微分方程理论：他和 Pardoux合作于 1990年发表的文章被认为是倒向随机微分方程理论的奠基性工作。Pardoux教授在公开发表的文章中指出彭实戈“在发现这个随机分析的新篇章中起了关键的作用。”
2.  创建了非线性 Feynman-Kac公式：这曾是一个非常基础但是长期以来进展甚小的数学问题：经典的 Feynman-Kac公式能不能推广到非线性情形？ 1992年彭实戈解决了这个难题，证明了一大类二阶非线性偏微分方程 (PDE)的解可以通过倒向随机微分方程的解来表示，从而获得了上述 PDE的轨道积分表示。而当 PDE线性时，此表示就是著名的 Kolmogorov-Feynman-Kac公式。
3. 获得一般随机最大值原理：非随机情况下最优控制的“ Pontryagin最大值原理”是现代控制领域的三个里程碑之一。彭实戈证明了一般随机最大值原理，被公认为解决了一个“长期以来的一个突出的公开问题”，是“最近二十年来两个主要进展”之一，被称为“彭最大值原理（Peng's maximum principle）”。
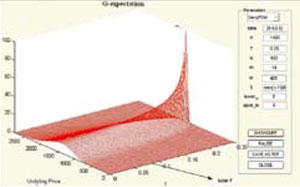
4. 建立了动态非线性数学期望理论：第一个一般意义下的动态相容的非线性数学期望是彭实戈 1997年引入的“ g-期望”，这种 g-期望保持了数学期望除线性以外的几乎一切性质。之后 1999年他通过独创的的方法获得了与经典的 Doob—Meyer的著名结果相应的 g—上鞅分解定理。

　　十多年来，倒向随机微分方程成为数学中一个非常活跃的前沿领域。彭实戈应邀去许多国际著名的高等学府（如普林斯顿大学、大阪大学、巴黎高工、苏黎世高工、庞卡莱研究所）讲学。 Pitman数学丛书 No.364《倒向随机微分方程》的序言一开始，主编 El Karoui教授写道： “自从倒向随机微分方程（BSDE）与1942年Ito教授引入的（正向）随机微分方程(SDE)的重要的不同是：SDE由当前确定的初始条件演化出将来的（当前无法确定）的解；而BSDE则由将来的（目前无法确定的终端条件）倒向地计算出当前能够确定的解。非常有趣的是：彭等引入的反射型BSDE可用来计算和分析很多类型的（涉及最优停时）美式期权定价问题。Pardoux和彭 1990年关于一般存在唯一性结果的奠基性文章（ Founder Paper）以来，倒向随机微分方程已经成为一个有趣的、活跃的和正在扩大的领域。 ”“它被证实在处理状态受限的问题上是强有力和优雅的 (powelful and elegant)工具”，“基于上述原因我们在巴黎六大概率实验室这是国际上顶级的概率研究中心）组织了 1995-1996学年的倒向随机微分方程研究班（每周一次）”。

非常有趣的是：彭等引入的反射型BSDE可用来计算和 分析很多类型的（涉及最优停时）美式期权定价问题。

　　新近，彭实戈引入了 G-期望和 G-布朗运动理论。该理论在 2005年挪威著名的 Abel Symposia国际学术研讨会上正式提出后已经获得了国际同行的重要反响： 2006年以来先后在中国丽江、法国 Evry和日本京等地召开的国际会议上作邀请报告 ; 2006年7月23-29日在德国 Jena举行的随机分析国际会议上破例邀请彭实戈用三个早上最佳时间就 G-期望和G-布朗运动理论作特邀系列讲演； 2007年5月日本大阪大学金融、保险研究中心 (CSFI)、大阪证券交易所开设的金融特别讲座，邀请彭实戈作为“特任教授”作系列讲演（ 12x 1.5小时），并全程录像播放，制成 DVD光盘。

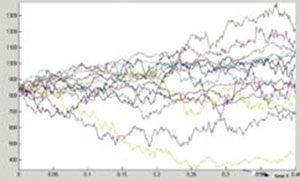彭实戈的在非线性数学期望研究的长期计划是创建和奠定非线性概率论的基础，推进相应的统计、随机分析及其在金融风险和其领域中的应用。这将推广 1933年由 Kolmogorov建立的现代概率理论。最近很多金融风险理论方面的专家呼吁金融领域的“第三次革命”（金融风险度量），而彭实戈提出的数学期望被认为是风险度量的重要工具。G-布朗运动的增量满足G-正态分布，一般要用非线性热方程来计算。与Bachelier和Einstein一样，彭最近引入的G-布朗运动仍旧是一个空间对称、增量独立且增量分布平稳的连续随机过程，而关键的不同是：G-布朗运动不是定义在Kolmogorov经典概率空间、而是在一个全新的次线性期望空间中，从而适于用作很多统计量不确定的过程的模型。

G-布朗运动的增量满足G-正态分布，一般要用非线性热方程来计算。	与Bachelier和Einstein一样，彭最近引入的G-布朗运动 仍旧是一个空间对称、增量独立且增量分布平稳的连续随 机过程，而关键的不同是：G-布朗运动不是定义在 Kolmogorov经典概率空间、而是在一个全新的次线性期 望空间中，从而适于用作很多统计量不确定的过程的模型。